Scoreholio Singles SPR Calculation Approximation
I recently attempted to reverse engineer the Scoreholio SPR change calculation that takes place at the end of every match. Below is what I found out.
Officially, all we really know is that it’s “like” the Elo rating system used for chess. We also know it was updated ~Nov 8th, 2022 to start taking individual performance into account for doubles matches when ScoreMagic is used.
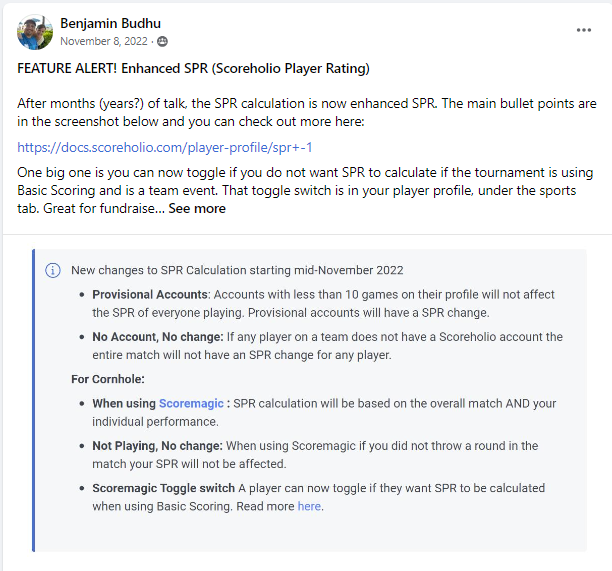
For simplicity, I started with singles games as a 1v1 match between 2 players should be an easier calculation than 2v2 with individual matchup performances considered. For now, I also ended with singles due to interest and time but it appears the formula below also applies to doubles matches where basic scoring is used (using each team’s average SPR as the single players’ SPRs).
Disclaimers:
- This is not the actual formula Scoreholio uses for SPR calculation!
- The formula below does seem to be very accurate for singles games played to 21.
- The formula will not work out of the box for doubles games using ScoreMagic
- The formula loses accuracy for singles games where the final score for the winner is something other than 21 (15,25,32,etc). (It gets close, but I haven’t nailed the correct way to scale the non-21 score base into the Score Diff term used)
- With a sample set of ~1700 singles games pulled from Scoreholio, the below formula got within ±0.01 of the actual SPR change recorded for over 99% of games.
The approximation formula:
Winner’s SPR Change ≈
[(Score Diff – SPR Diff) or 1] x [0.05 – (SPR Diff / 900)]
Important Note: If (Score Diff – SPR Diff) is less than or equal to 0, the first term becomes 1. See below for more details.
Terms:
- Score Diff = Winner’s Score – Loser’s Score (this will always be positive)
- SPR Diff = Winner’s pre-game SPR – Loser’s pre-game SPR (this will be positive if the higher SPR player wins or negative if there is an upset)
How I would describe what’s happening:
The formula above has 2 major terms, let’s dig into each:
- Term 1: [(Score Diff – SPR Diff) or 1]
- aka: Adjusted Margin of Victory
- aka: How much did the winner win by adjusted by how much they were expected to win by.
- In this setup 1 SPR = 1 Point, or in other words for every SPR point a player is higher than their opponent, Scoreholio thinks they should win by that amount.
- 1 SPR favorite = Scoreholio thinks you should win 21-20
- 6 SPR favorite = Scoreholio thinks you should win 21-15
- 15 SPR favorite = Scoreholio thinks you should win 21-6
- 21+ SPR favorite = You’re not going to get more than 0.03 SPR for winning (as this term becomes 1)
- As a favorite (player with the higher SPR), the winner is rewarded for each point beyond the expected margin of victory achieved.
- If the winner underperforms as the favorite (but still wins the game), this term simply becomes 1. In other words, Scoreholio calculates the change based on a 1 point margin of victory regardless of what the final score actually was.
- As an underdog (player with the lower SPR), the winner is rewarded for every point scored more than your opponent AND the difference in SPR is added on top as “bonus points”!
- In other words, if the winner is a 5 SPR underdog and wins the game by 5 points, Scoreholio calculates the change as if they had won by 10 points.
- Term 2: [0.05 – (SPR Diff / 900)]
- aka: The Multiplier
- After calculating the first term to see how many “points” the winner won by, we then convert those “points” to SPR by multiplying against this term.
- If 2 players start the game with the same SPR (SPR Diff = 0), then this term is simply 0.05. The first term is also simplified to just Score Diff when 2 players have the same SPR, so the SPR change will be (Score Diff x 0.05).
- For example, if 2 players have the same SPR and the final score is 21-11, the winner will get +0.5 SPR (10 * 0.05).
- When 2 players don’t have the same SPR, this term gets smaller when the favorite (higher SPR player) wins or larger when there is an upset.
- The divisor of 900 essentially converts every 9 SPR difference between the players into ±0.01 on top of the 0.05 base.
- For a 9 SPR difference:
- If the higher SPR player wins, this multiplier becomes 0.04
- If the lower SPR player wins, this multiplier becomes 0.06
- For an 18 SPR difference:
- If the higher SPR player wins, this multiplier becomes 0.03
- If the lower SPR player wins, this multiplier becomes 0.07
- For a 9 SPR difference:
- In short, the multiplier gets larger for an upset and smaller for an expected win. This translates to larger or smaller SPR changes even if the margin of victory remains the same. This is especially pronounced when the difference in SPR between the players is large.
- Putting it all together
- With an adjusted margin of victory (Term 1) and the multiplier (Term 2) determined, we simply multiply them together and round to 2 decimal digits.
- One thing to note is that SPR Diff is used twice in the equation, so an upset is rewarded twice and amplified by the SPR difference of that upset. Both the adjusted margin and multiplier are increased which is why you can see large swings in SPR after a big upset. On the other side, the margin and multiplier are both decreased if the winner is the SPR favorite which is why SPR only shifts meaningfully in the case of a large final point differential.
Example:
I thought about walking through a couple examples, but then decided it would be better for you to be able to create your own example using the above formula!
SPR Approximation Calculator:
- SPR must be between 35 and 95
- Winner must have score of 21
|
Player 1 SPR: Player 1 Score: |
Player 2 SPR: Player 2 Score: |
